Morpheus

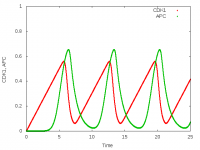
This model is a two-species version of the Xenopus embryonic cell cycle shown above that uses delay differential equations (Ferrell et al., 2011). It exhibits sustained limit cycle oscillations.

This model uses two Properties (CDK1 and APC) and two DelayProperties (CDK1_d and APC_d) with delay $\tau$. The latter are properties that return the value that has been assigned at time $t-\tau$.

The updated values of CDK1 and APC are assigned to (the back of) CDK1_d and APC_d using Equations. When these properties used in the DiffEqn, they return the value assigned in the past.

The two variables are logged and both a time plot and a phase plot are drawn.

• Explore the effect of delays by altering the DelayProperty/delay.

Ferrell JE Jr, Tsai TY, Yang Q. Modeling the cell cycle: why do certain circuits oscillate? Cell, 18:144(6), 2011.

This example model cell fate decisions during early patterning of the pancreas (de Back et al., 2012). The simple gene regulatory network of each cell is coupled to adjacent cells by lateral (juxtacrine) signaling.

The model defines a lattice of cells with a simplified hexagonal epithelial packing. This is specified in Space using a hexagonal lattice structure of size $(x,y,z)=(20,20,0)$ with periodic boundary conditions. The lattice is filled by seeding it with a Population of $400$ cells.

Each cell has two basic Properties X and Y representing the expression levels of Ngn3 and Ptf1a that are coupled in a System of DiffEqns.

The NeighborsReporter plugin is used to couple the cells to their directly adjacent neighbors. This plugin checks the values of X in neighboring cells and outputs its mean value in Property Xn.

This model uses a number of Analysis plugins:

• Gnuplotter visualizes the values of Y with a ColorMap that maps values to colors. It outputs to screen (interactive mode) or to PNG (local mode).
• Logger records the values of X and Y expression to file and, at the end of simulation, shows a time plot.
• The first HistogramLogger records and plots the distribution of X and Y expression cells over time.
• The second HistogramLogger records and, after simulation, plots the distribution of $\tau$, the time to cell fate decision (see reference).

• Change the lattice structure from hexagonal to square. See Space/Lattice.
• Change the strength of lateral stabilization b and observe the pattern. See CellTypes/CellType/System.
• Change the noise amplitude and observe time to cell fate decision ($\tau$).

W de Back, J X Zhou, L Brusch, On the Role of Lateral Stabilization during Early Patterning in the Pancreas, Journal of the Royal Society Interface, 10:79, 2013.