Morpheus

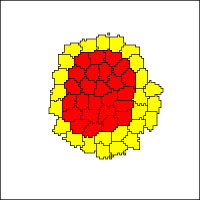
This model shows the original cellular Potts model (a.k.a. Glazier-Graner model) of cell sorting based on the Steinberg's differential adhesion hypothesis.

Two CellTypes are defined, each of which has a VolumeConstraint specifying the cell's target area/volume. In the CPM element, the MetropolisKinetics can be configured and the Interaction energies between cell types are specified.

Although cells can be initialized as single points using e.g. the InitCircle plugin, in this example, the Nodes of each Cell in the CellPopulations are given explicitly. In fact, these Populations are restored results of a previous simulation.

The simulation shows two populations of spatially resolved cells that initially organized in a mosaic fashion. Through differential adhesion, the motile cells sort out and re-organize into an distribution in which one cell type engulfes the other.

Snapshots of the simulation are saved to files named [Title][Time].xml.gz. These files containing intermediate and result states can be opened and used as initial conditions for new simulations. Remember to change StartTime and StopTime accordingly.

Graner F, Glazier J. Simulation of Biological Cell Sorting Using a Two-Dimensional Extended Potts Model. Phys. Rev. Lett. 69 (13): 2013–2016, 1992.

This model show a simulation of a growing cell population, using the cellular Potts model.

This model specifies CellType which has a VolumeConstraint and a Proliferation plugin.

In the Proliferation plugin, the Conditions for a cell to divide are given. Here, each cell that has more than 90% of the target volume has a small probability to divide. Once a division has taken place, the Equation defined in the Triggers elements are triggered.

extern>http://imc.zih.tu-dresden.de/morpheus/examples/CPM/Proliferation_2D.xml

In Morpheus GUI: Examples → CPM → Proliferation_2D.xml

This example shows self-organized collective motion of cells as a result of persistence ('cellular inertia'). A similar model has recently been used in (Czirok et al., 2013).

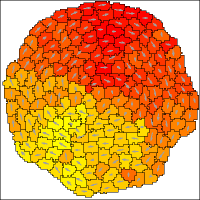
The model uses the Persistence plugin that causes cells to prefer to move in their current direction. The direction is stored in a PropertyVector that is used to plot the color and arrows in Gnuplotter.

The model is simulated in a circular domain with constant boundary conditinos, which can be set up in Lattice / Domain / Circle. The value for the constant boundary is specified in CPM / BoundaryValue.

• Change the boundary conditions from circular=constant to x/y=periodic and observe the resulting collective motion.
• Change the decay-time of Persistence (specifying the 'memory').

Czirók A, Varga K, Mehes E, Szabo A, Collective cell streams in epithelial monolayers depend on cell adhesion. New J. Phys. 15 075006, 2013.

This model show a CPM simulation of a growing cell population in 3D.

This model specifies CellType which has a VolumeConstraint and a Proliferation plugin. In the Proliferation plugin, the Conditions for a cell to divide are given. Here, each cell that has more than 90% of the target volume has a small probability to divide. Once a division has taken place, the Equation defined in the Triggers elements are triggered.

In this model, two medium cell types have been defined. One of these (called matrix) is used to represent a matrix with higher adhesivity. This is done by (1) defining the 'matrix' cell type as a BoundaryCondition of the -z boundary in the CPM and (2) providing lower contact energy for cell-matrix interaction than for cell-medium interactions.

The simulation is visualized using the TiffPlotter that saves TIFF image stacks that can be loaded by image analysis software such as Fiji and displayed using Fiji's 3D Viewer plugin.

extern>http://imc.zih.tu-dresden.de/morpheus/examples/CPM/Proliferation_3D.xml

In Morpheus GUI: Examples → CPM → Proliferation_3D.xml

This example models a single cell that moves according to a Levy walk: a random walk with occassional occurrence of long straight walks.

The model defines a CPM cell that has two properties:

• A PropertyVector that gives the direction of movement and
• A Property that defines the time when this direction of movement is changed.

The change in direction is using a VectorRule. In this case, it specifies a new random direction for each of the 3 x,y,z coordinates separately: move_dir = sin(angle), cos(angle), 0 where angle = rand_uni(0, 2*pi).

This is calculated with an Event. Upon triggering, this sets the new direction and a waiting time until the next change of direction. To model a superdiffusive Levy walk, this waiting time is chosen from an exponential distribution: change_time = time + 20 * rand_gamma(0.5, 5)

Finally, the cell is made to move in the chosen direction using DirectedMotion that takes the PropertyVector as input.

extern>http://imc.zih.tu-dresden.de/morpheus/examples/CPM/RunAndTumble.xml

In Morpheus GUI: Examples → CPM → RunAndTumble.xml

This illustrative example shows the emergence of clonal populations from stem cells in an intestinal crypt. Stem cells in the bottom of the crypt divide asymmetrically and produce a population of transit amplifying (TA) cells. For each of the TA cells, the color indicates the stem cell is it derived from.

This model shows several new modeling features, available as of Morpheus 1.2.

The crypt-like domain is specified by loading an external 8-bit TIFF image file using Lattice/Domain/Image.

Stem cell divide asymmetrically using the new ChildID handles in the Proliferation plugin. This sets a user-defined symbol (here: daughter) to either 1 or 2 that can be used to distinguish both daughter cells. This symbol is then used to set the stemness s of one daughter to 1 and the other to 0: s = if(daughter==1, 1, 0).

When a cell looses its stemness s, it is moved to the TA cell type. This is done using the new ChangeCellType plugin.

Upon satisfyiug its Condition, ChangeCellType move the cell to te specified new cell type. By default, all the properties of a cell that exist in both cell type context are maintained and nuspecified ones are set to their default values. This default behavior can be overridden in Triggers by specifying Rules stating how to deal with specific properties.

The new PopulationReporter allows the collection of statistical data about the cell population. Here, it is used to count the sizes of the various clonal populations. This number of reported into a Global and subsequently written to file and plotted using a Logger.

extern>http://imc.zih.tu-dresden.de/morpheus/examples/CPM/Crypt.xml

In Morpheus GUI: Examples → CPM → Crypt.xml